Okul Öncesi ve Kıdemli Okul Öncesi Dow Grubu Çocuklarının Matematiksel Bilgisini Öğretme Modern Yöntemleri için Temel Gereksinimler, Oyun Yöntemleri, Çocuklarla Matematiksel Eğitim Yöntemleri, Geride Geri Dönüş ve Öğrenmede Başarılı: Açıklama:

Çocukları eğitmek ve matematiksel becerilerini öğretmek için metodoloji bu materyalde açıklanmaktadır.

Makalenin içeriği

Çocuğun beyninin tam gelişimi, çevre hakkındaki yeterli algısı, yaşamın ilk birkaç yılında geçici uzay formuna yönelmesi. İnsan düşüncesinin diğer tüm aşaması, çocukluktaki mantık yasalarının nasıl öğrenildiğine bağlıdır.

Matematiksel Kavram: Okul Öncesi Çocuklarda Oluşumu İçin Yöntemler

Becerilerini eğitmek, deneyim biriktirmek, çocuğun akıl gelişir. Ve bu önemli rolde matematiksel bilgidir. Öğretim yönteminin ve pratik ipuçlarının hesaplanmasına uyum sağlamak için toplumun kolektif görevi.

Matematiksel kavram, bir bütün olarak matematik hakkında temel bilgi veren malzeme sempatik işlevine odaklanan bir dizi egzersiz ve göreve dayanmaktadır. Öğretmenler, matematiksel becerileri öğretme ve edinme sürecinde bu çocukla başa çıkmaya yardımcı olur.
Zaten bir çocuğu eğitmenin ilk yılında davranış disiplinine hakim olmak, Görevleri net bir şekilde açıklama ve ortaya çıkan soruyu cevaplama yeteneği. Yetkili metodolojik hazırlık sayesinde, çocuk sayısal seri, hacimler ve değerler, zaman aralıkları hakkında bilgi edinir.
Toplama ve çıkarma, çarpma ve bölünme konusunda eğitilmiştir. Görevlerin çoğu eğlenceli bir şekilde gerçekleşir ve çocuğun dikkatinin konsantrasyonunu öğrenme konsantrasyonunu korumanızı sağlar: röleyi geçme, matematiksel rebusların çözülmesi, görevlere katılım.
Görevleri çözmek için, öğretmen gruplara ayrılma yöntemini kullanır - bu bir okul öncesi çocukları eğitmenizi sağlar. kolektif etkileşim. Çocuk yargılarını tartışmayı, başkalarının eylemlerini analiz etmeyi ve sonuç çıkarmayı öğrenir. Hataları tanımayı ve düzeltmeyi öğrenir. Yardımcı malzemeler kullanın: tablolar, sopalar, cetvel, geometrik nesneler.

Okul öncesi

Öğretmen ayrıca, çocuğun eğitim kurumunun dışındaki ustalaşmış materyali pekiştirmesine izin veren ek görevler de verir. Ödevler için - Ders kitapları, pratik çalışmalar için defterler.
Eski gruplar için bilgisayar programları geliştirmek. Öğretmen, çocuğun zaten edinilmiş deneyimini dikkate alarak her yeni görevi seçer. İncelenen materyalin tekrarlanması, okul öncesi okulun yeni bir ders vermesine yardımcı olur.
Ebeveynleri materyali birleştirme sürecine dahil etmek yararlıdır. Bunun için öğretmen ebeveynlerle danışmanlık çalışması yapar. Bu aşamada, çocukta gelişimin ne kadar hızlı olduğunu belirleyebilirsiniz - akranlarının önünde veya gecikiyor. Ek bireysel sınıflar gerekli olsun ya da olmasın.
Çocuklara bilgi sunumu, anlayış düzeyinden daha yüksek olmamalıdır. Karmaşık terminolojiden kaçınılmalıdır. Öğretmen, iyi bir çalışma için bir okul öncesi çocukları teşvik etmelidir - bu, en iyi sonuçları elde etmek için uyarır.

ÖNEMLİ: Sıcak mevsimde, gayri resmi bir ortamda yazılım materyalinin geliştirilmesini tercih etmeye değer - yürüyüşler, kampanyalar, çocuk kampları. Sınıfta, çocukların yaşı ve görevler dikkate alınarak görsel materyaller kullanılmalıdır.

Malzemeler renkli ve çekici olmalıdır. Yeterli sayıda farklı form. Nesneler görevlere uygulanmaya uygundur. Öğretmen, matematiksel bileşenin başında olacak şekilde ödev için komut dosyasını ayarlamalıdır, ancak aynı zamanda sıkıcı görünmez. Bu yöntemlerin bütünlüğü, bir çocuğu okulda çalışmaya başlamak için gerekli matematiksel görevlerin geliştirilmesinde daha zor bir aşamaya geçmeye hazırlar.

Farklı yaş gruplarındaki çocuklarla modern çalışma yöntemleri için temel gereksinimler

Her grup için eğitim programını konularda analiz etmek önemlidir:

hacimler ve değerler
uzamsal yönelim
geometrik figürler
sayıların Temsilcileri
geçici alan
miktar

Erken yaşta çocuklar, iletişim becerilerini ve toplumda adaptasyonu geliştirmek için kendi kendine eğitim ve matematiksel temeller bilgisine ilgi gösterirler. Buna dayanarak, okul öncesi ve eğitim kurumlarının erken matematiksel gelişime katkıda bulunan bir metodoloji geliştirme ve uygulama görevi. Görevin özü, okul öncesi dönemde çocuklarda matematiksel gelişim için modern gereksinimleri yerine getirmektir.

Okul Öncesi Grubunun Matematiksel Gelişimi için Ana Modern Gereksinimler

İlk matematiksel beceriler Çocuk yaşta ustalaşabilir dört yıl. Bu, görevleri oynak bir şekilde ustalaşma sürecinde olur. Öğretmen, oyunun dahil edilmesine katkıda bulunan çocuğun etrafında bir atmosfer yaratmalıdır. Temel hesaplamaları belirlemek için görsel ve sözlü bir değerlendirme kullanmaya yardımcı olan önde gelen sorular sormak: biçim, boyut, geçici alan, miktar.

Çocuğun karşılaştırmalı veya gruplandırma eylemleri gerçekleştirmesi için bir görev zinciri oluşturmak. Oyunun bir dizi unsurunu yeniden yarattı. Nasıl sayılacağını biliyordu. Oyun sırasında çocuğun eylemlerini inisiyatif olarak gönderin.

Daha büyük sonuç için cesaretlendirmeyi motive edin. Çocuk didaktik materyaller, bilişsel oyunlar, mantıksal düşünme geliştirmeli: renk küpleri, piramitler, geometrik bulmacalar, transformatör figürleri, sopalar, nesnelerin nesneleri.

Okul öncesi

Bu beceri için temel oluşturacak:

nesneleri gruplara bağlayın
bunları şekil, renk, miktarda ayırt edin ve dağıtın
bir öğeyi karşılaştırarak hariç tutun veya yapın
eksik öğeyi değerlendirin ve bulun
eylemleri tanımlayın ve daha fazla hareket hakkında konuşun

Beş yaşın altındaki çocuklarda matematiksel kavramların gelişiminin konuşma ve bilişsel yetenekler üzerindeki etkisinin sonuçları:

Sayılar ve Sayılar Hakkında Fikirler - Sayıların ezberlenmesi ve tanınması, on yüksek sesle sayma yeteneği. Sayısal gruplarda sayının seri atamasında, nesnelerin oluşumunda gezinin. Nesne sayısını karşılaştırın. Sorunları çözme eylemiyle ilgili soruları cevaplayın.
Nesnelerin özellikleri - Uzunluk ve yüksekliğe göre tanım, genişlik ve kalınlığa göre karşılaştırma, kütle ve hacim anlayışı. Geometrik şekilleri tanıma, yapılarını belirleme yeteneği. Nesneleri kendi aralarında gruplar halinde bağlamak için. Nesneli bir dizi manipülasyon seslendirin.
Karşılaştırmalı ilişkiler - Nesnelerin şekil, renk, sayı dağılımı. Nesnelerle geçici ve mekansal bağlantıların oluşumu. Özelliklere göre sıralı zincirler oluşturmak. Konuşma ve Karşılaştırma aşamalarını zaman çerçevesine ifade etme yeteneği.
Miktarların değişmezliği kavramı - Konum ve geçici segment ne olursa olsun, uzaydaki nesnelerin görsel algısı ve değerlerinin korunması. Bir nesnenin varlığını ve geçici alandaki özelliklerini sözlü olarak yansıtma yeteneği.

Becerilerin geliştirilmesi

Kıdemli Okul Öncesi Grubunda Matematiksel Temsillerin Oluşumu

Hesap ve miktar

Kıdemli Okul Öncesi Grubunun eğitim kavramı Çocuğun sayı ve hesaplama bilgisini genişletmek.

Öğretmen her sayıyı ayrı olarak açıklar. Dikkat 0 ve 10 gibi sayılara odaklanmak.
Sayısal serideki oluşum ve konumlarının sırasını açıklar. Eğitim sırasında görsel örnekler kullanılır, görselleştirme ve göz eğitilir.
Sayısal serileri karşılaştırarak, çocuk yeni oluşumları ve sayıların tanımlarını öğrenir. Uygulamada, sayının nesnelere uygulanması. Numaranın grafik görüntüsünü hatırlar.
Tüm okul dönemi çocukları pratik görevleri sayılarla gerçekleştirir - dikkat etme, hatırlama, analiz etme ve yerine getirme yeteneği. Öğretmen, sayısının sayısal satırdaki yerinden görünmezliğini açıklar.

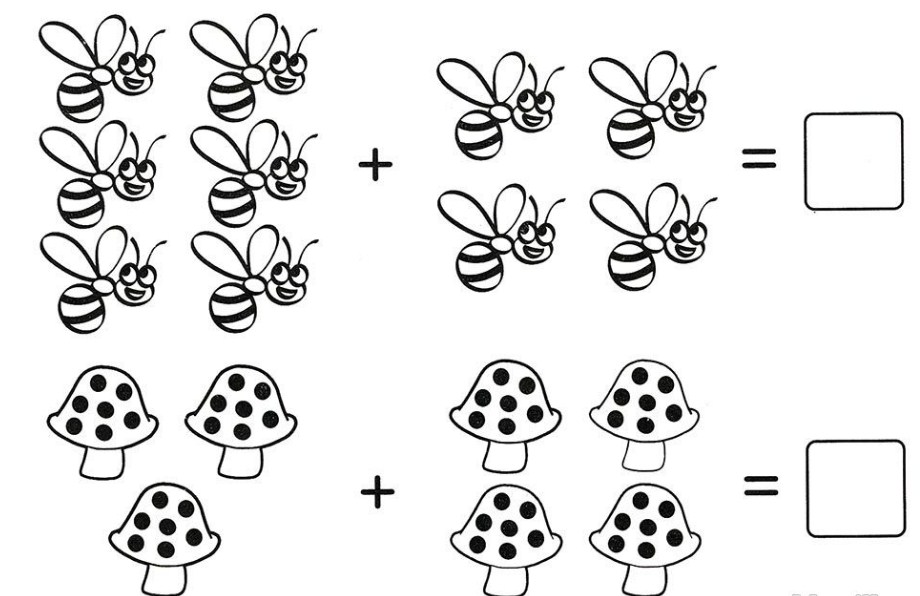
Kontrol etmek

Nesnelerin değeri ve hacmi, nesneler arasındaki mesafe sayının kendisini etkilemez. Bu, çocuklarda sayının bağımsızlığı hakkında bir fikir oluşturur, herhangi bir referans noktasından farklı yönlerde sayılmayı öğretir. Seri skoru ve yönü emilir.
Tüm sayının anlaşılması da geliştirilir ve parçalara ayrılır. Netlik için, öğretmen örnekler kullanır: bir elmayı yarıya indirmek veya sayfayı birkaç parçaya bükmek.

Geometrik şekillerle tanışma

Kıdemli grupta, edinilen materyale yeni formlar eklenmeye başlar. Zaten bilinen geometrik formlar için yenileri eklenir.

Bir figürü diğerine uygulayarak, çocuklar birinin diğerinden benzerliğini ve farklılıklarını belirler. Öğretmen, figürlerin nesnelerle benzerliğine örnekler verir: top - yuvarlak, yumurta - oval şekil.
Bir rakam ortaya çıkıyor - bir dörtgen. Bir dörtgen figürü ve özellikleri hakkında anlayış oluşur. Önemli belirtilerde, çeşitli formların karşılaştırmalı bir analizi yapılır. Dolayısıyla öğretmen üçgen bir formla karşılaştırıldığında, dörtgen tanımının oluşumuna yol açar.
Görev, hangi rakamların dörtgen olarak adlandırılma hakkına sahip olduğunu bağımsız olarak sonuçlandırmaktır. Pratik sınıflar yöntemiyle, çocuklar nesneleri diğer anlamları dikkate almadan işaretlerden birine göre gruplamayı öğrenirler. Okul öncesi çocuklar eylemlerini tanımlama yeteneğini geliştirir.

Geometri

Çevresel nesnelerde geometrik formlar bulmayı öğrenirler, illüstrasyonlarda tanınırlar. Öğretmen, okul öncesi çocukları çeşitli doğru ve düzensiz şekillere tanıtmalıdır: dikdörtgen üçgenler, eşkenar, ikizkenarlar; Quadrangles - Kareler, eşkenar dörtgenler, dikdörtgenler.
Geometrik malzeme ile yapılan deneyler, okul öncesi çocukların daha fazla matematiksel anlayışını etkiler: gruplar üzerindeki nesneleri önemli işaretlere göre karşılaştırma ve sınıflandırma, benzerlikleri ve farklılıkları belirleme yeteneği.

Ölçüm ve boyut

Yaşlı grubun okul öncesi çocuklar, değerlerin belirlenmesinde zaten yeterli deneyime sahiptir- nesnelerin kendi aralarındaki uzunluk, yükseklik, genişlik karşılaştırması.

Kendi aralarındaki bireysel boyutlardaki nesneler arasındaki benzerliği ve farkı nasıl gruplandıracaklarını, kolaylaştıracaklarını, nasıl bulacağını biliyorlar. Göreve sözlü bir yanıtın nasıl formüle edileceğini biliyorlar.
Ayrıca, talimat koşullu bir önlem kullanılarak eğitim programına dahil edilmiştir. Pratik sınıfların yardımıyla çocuklar, sıvıların ve dökme cisimlerin hacmini, nesnelerin boyutunu belirlemeyi öğrenirler. Uzun değerleri ölçerken, öğretmen çocukları değerleri ölçmek için temel kurallara sokar- ölçümü gösterir.
Ölçümün başlangıcını ölçülen nesneyle uygulayarak ve karşılaştırarak nasıl doğru kullanılacağını gösterir. Ölçüm sonucunun nasıl kutlanacağını ve hesaplanacağını söyler. Çocuklar bağımsız olarak öğrenmeli ve ölçüm eylemlerinin sırasını doğru bir şekilde gözlemlemelidir. Toplu ve sıvı bileşenleri ölçmek için, yardımcı ölçüm nesneleri kullanılır - bir kaşık, bir fincan, bir bardak.

Biz ölçeriz

Öğretmen, ölçüm seçeneklerini açıkça gösterir - tam bir cam, yarım bardak. Hesaplama tekniğini gösterir: ölçülen her cam bir kenara bırakıldıktan sonra, bir öğe döşenir, nesneler gözlük sayısı anlamına gelir. Tüm süreç çocuklar için açıkça görülebilecek şekilde ölçüm öğeleri iyi görülebilir olmalıdır.
Malzemenin daha iyi emilimi için ölçüm cihazlarını, alternatif ölçüm nesnelerini çeşitlendirmelisiniz. Bu, konudaki önlem sayısının nasıl belirleneceğini öğrenecek, ölçüme eşit parçanın nasıl ölçüleceğini, nesneleri ölçüm sonuçlarına göre birbirleriyle karşılaştıracaktır. Ölçümlerle çalışmak, çocukların bir sayının oluşumu ilkesini anlamalarını sağlar.

Mekansal ve geçici yönergeler

Ana görev - çocuklara yerlerini belirlemeyi öğretin, Hareketin yönünü hatırlayın, arazide gezin. Çocuk, nesnelerin hangi tarafında olduğunu anlamalı, bunu sözlü olarak ifade etmelidir. Haftanın günlerinin adına hakim olmak için takvim hesabı, zaman aralıkları. Çocuğun uygulama yöntemi, yerleşik döneme göre eylemler yapması öğretilir. Zaman çerçevesini kendisi koymaya çalışır. Bu disiplinin geliştirilmesine yardımcı olur.

Matematiksel eğitim tekniklerinin değerlendirilmesi

Çocuklarda soyut düşünme ve analitik yetenekler geliştirmek için öğretmen inisiyatif göstermeyi mümkün kılar. Malzeme ilgi çekici, eğlenceli bir biçimde sunulur. Bir çocuğu sürece bağlamaya teşvik eder - düşünün, kararlar verin, eylemleri haklı çıkarır. Görsel malzemeler kullanılır.

Uygulamalı öğrenme mekanizmaları

Yöntem, pratik görevlerle çocuklarda matematiksel becerilerin geliştirilmesi. Öğretmen gerekli materyali sağlar: örnekler, sayma öğeleri, geometrik şekiller, ölçümler.

Davranış Uygulaması

İletişim sınıfları iki şekilde gerçekleşir:

Bireysel eğitim - Öğretmen çocuğun gelişiminin özelliklerine odaklanır. Bilginin algılanması ve yürütülmesi sürecini kontrol eder. Görsel örnekler yapar. Çocuğun diyaloğunu içerir. Bağımsız kalkınma için ek görevler verir.
Grup çalışması - Bilgi sunumu ekipte gerçekleşir. Görevler bir gruba veya çiftler halinde dağıtılır. Öğretmen netlik için didaktik malzemeler verir. Grubun tüm üyelerinin etkileşimi gerçekleştirilir. Sonuçlar karşılaştırılmıştır.

Kolektif sınıflar

Görevler her yaş grubuna uymalıdır. Yeni olanı pekiştirmek ve ustalaşmak için tamamlanan malzemeyi birleştirin. Görevin çeşitli görevlerini birleştirin. Eylemlerde bir artış olarak karmaşık. Pratik görevler, birbirine bağlı olarak yıllık eğitim programı ile birlikte ele alınmalıdır.

Egzersiz Çeşitleri

Müfredat şu:

Tekrarlanabilir eylemler - Öğretmen ödevin yürütülme kuralını belirler. Bir eylem örneği gösterir. Yürütme süresini koordine eder. Çocukların gerekli tüm koşulları yerine getirme görevi.
Etkili Eylemler - Öğretmen görevi seslendirir ve çocukların doğaçlama yapmasına izin verir. Çocuk eylem üzerinde düşünmeyi öğrenir, çözümleri seçer, deneme yanılma yoluyla doğru seçeneğe gelir. Öğretmen nadiren ipuçlarını kullanarak bir gözlem işlevi gerçekleştirir. Çocuklar kendi başlarına sonuna kadar gelmelidir.

Matematiksel bilginin eğitiminin bir parçası olarak oyun teknikleri

Çocuğu eğitime uyarlamak için bir oyun kullanılır. İncelenen bilgiyi güçlendirmek için sözlü ve maddi oyunlar kullanılır. Eğitim Oyunları - Yeni Becerilerin Tanıtımı için.

Oyun türleri

Matematiksel dersler oyun türleriyle birleştirilir:

Entelektüel - Geliştirme, hızlı fikirler oluşturma.
Dinamik - Dokunsal duyumlar ve sözlü eşlik yöntemiyle bilgiyi düzeltmeye yardımcı olur.
Sahneli oyunlar - Matematiksel bilginin gerçek hayatta etkileşimini ve uygulanmasını anlamanıza izin verir.

Oyun ana görevden uzaklaşmamalıdır - programın asimilasyonu. Ve öğretim materyalleri ile birleştirin.

Sözlü ve kanıt teknikleri

Eğitimde ek yöntemler:

Sözlü yorumların eşlik ettiği görsel bir gösteri. Öğretmen çizimler, nesneler, netlik eylemleri kullanır. Onlara ağızdan bir karakteristik verir.
Görevi yorumlama ve belirleme. Görevin ve prosedürün ayrıntılı bir açıklaması için kullanılır. Grubun yaşına bağlı olarak, bilgiler tam veya aşamalar halinde gönderilir.
İlişki yöntemi. Öğretmen, incelenen materyalle ilgili bir dizi konu temelinde çocuklarla bir diyalog kurar. Soruların bir kısmı, çözümün başka bir kısmı olan görevdeki nesneleri ilgilendirmelidir. Sorular anlaşılabilir olmalı, karmaşık konuşma dönüşleri içermiyor. Ayrıca, çocuklar kendileri soru sorabilmelidir. Görüşme toplu veya bireysel olarak gerçekleştirilir. Soruların cevapları açık ve kapsamlı olmalıdır.
Öğretme teknikleri
Sözlü rapor Adım -adım eylemleri ve sonucunun bir açıklamasından oluşur.
Gözlem, analitik karşılaştırma, özetleme. Görsel karşılaştırma tekniklerine hakim olan çocuklar gözlem yöntemini kullanırlar - nesnelerin veya bireysel grupların ayırt edici özelliklerini tanırlar. İşaretlerin benzerliğini birleştirmek için karşılaştırma uygularlar. Bu becerileri kullanarak, çocuklar yapılan işi özetlemeyi öğrenirler. Bu, ödevin özünü nasıl belirleyeceğinizi öğrenmenizi sağlar.
Matematiksel anlamda sistematizasyon. Öğretmen çocuklara matematiksel bilginin evrenin sisteminin bileşenlerinden biri olduğunu açıklamalıdır. Çocuklar soyut düşünmeyi öğrenir, sistematiktir - bu da beyin fonksiyonlarını aşırı yüklemeden matematiksel yetenekler geliştirmenizi sağlar. Sistematizasyon pratik sınıflarda kullanılır - öğretmen çeşitli modelleri gösterir: üç boyutlu, sayısal, zaman çerçeveleri. Ders sırasında, öğretmen materyali incelemek için birkaç taktik içerir - bunlardan biri sistematizasyondur.

Geciktirme ve öğrenmede başarılı çocuklarla matematik eğitim yöntemleri

Malzemeye hakim olmanın gecikmesi:

Yöntem, oyun tekniklerini kullanarak çocuğun dikkatini sınıflara çekme görevine dayanmaktadır.
Ek bireysel görevler gerçekleştirilir.
Malzeme, çocuğun öğrenebildiği hızda sunulur.
Ayrıca, günlük yaşamda bilginin konsolidasyonu çözülmektedir. Ebeveynlerle önerilen görüşmeler yapılır. Ebeveynleri olan bir çocuk için ayrı görevler geliştirilmektedir.
Dikkat, azim, öz kontrol gündeme getirilir. Bir teşvik ve motivasyon sistemi kullanılır.
Görevler aşamalarda karmaşıktır - çocuğun akademik performansına bağlı olarak.
Toplu çalışma, gecikme yetenekleri olan çocuklar ile öğretmen ek dikkat sağlar: soruların cevapları, eylemlerin bireysel olarak ayarlanması.

Akademik performansa bağlı olarak

Hızlandırılmış Algı:

Hızlandırılmış bir öğrenme algısı durumunda, öğretmen genel kolektif görevden ayrılmadan çocuğun görevini karmaşıklaştırır.
Çocuğu akranlarla etkileşime girmeye yönlendirir.
Disiplin, tasarım yükseltir.
Ödevin kesin performansını düzenler.

Çocukların matematiksel gelişimi için baskın faktör, elverişli bir ortamın yaratılmasıdır. Eğitime modern yaklaşımlar temelinde tasarlanan oyun yöntemleri, bu görevle iyi başa çıkmaktadır. Bu teknik, onunla başa çıkma arzusunu itmeden çocuğun beynini aşırı yüklemeden malzemeye hakim olmanızı sağlar. Oyun sayesinde çocuklar ev ortamında matematiksel bilgileri ustalaşabilir ve birleştirebilirler. Tüm bu faktörler bir çocuğu daha zor bir aşamaya hazırlamaya yardımcı olur - okulda eğitimdir.